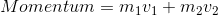Partners: Chong and Aiqi

Introduction/Theory:

The purpose of this lab is to find the swing period of multiple objects. The objects we will be finding the period of are a triangle, half-disk, ruler, and ring. The triangle and half-disk will have two different inertia we’ll be measuring, which are based off of their different pivots. Here is the pivots we will be going about:

 

Before class we were asked to find the period of these objects theoretically. In order to do this we first had to calculate the Inertia about the pivot for each object. After getting the inertia we would plug in our two known variables, torque and inertia, into our torque equation (torque = Inertia*angular acceleration) and solve for angular acceleration.  Since we also know angular acceleration is equal to (angle * “angular velocity” ^2) we fuse our two equations together and solve for angular velocity. After solving for angular velocity we solved for period which is (2π/ω)

Here is the example calculations for each object:

Ring’s theoretical calculations for period:

Meter stick’s theoretical calculations for period:

 

Triangle’s theoretical calculations for period (Orientation 1):

 

Triangle’s theoretical calculations for period (Orientation 2):

 

Half-disk’s theoretical calculations for period (Orientation 1 + Orientation 2):

 

Experimental/Procedure:

Here is an example of the basic apparatus we were using:

 

The object is held up by a pole stand set up. On a horizontal rod attached to the  pole stand was a taped down paper clip bent into a shape of a hook that the objects would pivot off of. Taped to the bottom of the object is a piece of tape so that the motion detector doesn’t get confused what it’s sensing (make the tape thin or the motion sensor will calculate the period wrong). Since the triangle and half-disk trials don’t have natural holes at the pivot points, we taped paper clips to each side of their pivot points to form an opening that the rod hook could go through and to try and reduce swinging in any direction that’s not where it should be swinging. Another pole stand was used to hold a motion detector that recorded the swing period of the object.

Holding up the ring was a special case however. It came with its own attachment we had to clamp onto the pole stand separately. Holding up the meter stick was also a special case since the pole stand was way too small for the experiment, so for the meter stick we used a large pole stand.

During each trial we swung the object a small distance (about 15 degrees) on their respective pivots and recorded the period of its swing using the motion detector on LoggerPro. We took the average period of the graph on LoggerPro for a more accurate result.

Here is what a typical graph looks like:

We wrote down the periods for each object and compared it to our theoretical predictions:

 

Conclusion:

Overall the lab was a success. Our percent errors were astonishingly quite low, with the triangle’s 1.34% error being the highest among the objects. These low percent errors are probably due to the minimal amount of systematic errors present in the lab, but there are always some. Some systematic errors that caused the difference in results include the rotational friction present. This would increase the period over time since the swing motion would be slowed down as it rotates. Also another error that we assumed true was the Taylor Series proof that sin(Ѳ) is approximately equal to Ѳ at small angles. This is not quite correct but we assumed it to be true in the lab because we were working with small angles. One more error that affected the lab was the piece of tape used to detect the period of the objects. The way the motion detector works is that it waits for a change material/color to log a period so the motion detector actually adds onto the period of the object a bit due the width of the tape traveling across it’s sensors. We try to minimize this by folding the tape in half but this discrepancy is still prevalent.

 

 

 

 

Partners: Chong and Aiqi

Theory/Introduction:

The purpose of this lab is to determine the moment of inertia of a right triangular thin plate around it’s center of mass for two perpendicular orientations of the triangle.

We will be determining the Inertia using an experimental method and a theoretical method, then compare the results. The theoretical way of calculating the inertia about the rotation around the center of mass is by using the parallel axis theorem and solving for I_cm. We calculated the Inertia about the side of the triangle by making making small dI’s of the rotation of several small rods that made up the triangle then integrated them.  After finding the inertia around the edge we implemented the parallel axis theorem.

Our experimental approach involved taking the inertia of the disk system alone then taking the inertia of the disk-triangle system. Subtracting the disk system from the disk triangle system will give us the inertia of the triangle.

Experimental Procedure/Apparatus:

First we made sure to get the dimensions of the triangle along with the mass.

We mounted the triangle on a holder and  the upper disk. The upper disk floats on a cushion of air. A string is wrapped around the pulley on top of and attached to the disk and goes over freely-rotating “frictionless” pulley to a hanging mass. The tension in the string exerts a torque on the pulley-disk combination. By measuring the angular acceleration of the system we were able to determine the inertia of the system (just like our last lab).

We followed the same experimental procedure as the last lab to get our angular accelerations.

Analysis:

Here we took the average of the accelerations going up and down and plugged the values into our inertia equations (same equations from last lab):

Here is our theoretical vs. our experimental results:

Conclusion:

Overall our lab was a success. Our percent errors for each triangle were fairly close experiment 1 had 4.4% and experiment 2 was 2.5%. One of the systematic errors that helped cause this percent error was the fact that the disks rotation was not actually frictionless, this caused the experimental values to be lower than our calculated values. The experimental value was also lowered from the air drag caused by the triangle’s rotation. Even with these errors however, we were still able to get a good estimate of the inertia of the triangle along two different orientations.

 

Partners: Chong and Aiqi

Theory/Introduction:

The purpose of this lab is to test how the conservation of energy and angular momentum apply to a ruler on a pivot that is released into a swing where it picks up a clay block from the ground and travels up.

In order to do this experiment we will be making equations based on four points during the swing. Right after it is let go, right before it makes impact with the clay, right after it makes impact with the clay, and when the new meter-clay system reaches its maximum height.

We went into this lab knowing that before the ruler is released all of its energy is stored as GPE, before/after impact with the clay all of its energy is rotational kinetic energy, and when the final height of the meter-clay system is reached all the energy is stored as GPE once again.

Apparatus/Procedure:

To set things up we attached a motion detector to a pole and attached the pole to the ruler’s hole at the 20 cm mark which will act as our pivot. On the bottom of the ruler will be taped down paper clips pointed to puncture the clay block that will be right underneath the pivot point on the floor. We made sure to measure the mass of the meter stick and clay block and also measure the height off the ground of the center of mass. Here is what the set up looks like:

Once everything is set up we took the video and started the experiment. We had the ruler let go from horizontal and proceeded to watch it puncture the clay and take it to a max height. After we uploaded the video onto LoggerPro and got the height of the object by going frame by frame until it reached peak height. Slow motion videos are recommended since it gives you a more exact maximum height. Make sure to scale the video to something, we used a ruler in the background.

 

Our experimental maximum height turned out to be 0.3299 meters.

Analysis:

After getting the experimental height we compared it to our theoretical height. In order to get theoretical height we made a conservation of energy equation involving the initial energy of the GPE when the ruler is at horizontal and the final energy of the rotational kinetic energy in order to find the angular speed of the ruler before impact with the clay. However, we have to solve for the inertia of the meter stick since its needed for the rotational KE equation. This is done by using the parallel axis theorem and solving for the Inertia around the axis of rotation. Once we have the final angular velocity before it hits we have to solve for the angular velocity after it hits the clay. This is done by setting up a conservation of angular momentum equation from right before impact equal to right after impact. However we had to get the inertia of the new system which is just the added on inertia of the clay around the pivot (clay is considered a point mass).

 

After getting the angular velocity we made a  conservation of energy equation again, but this time the initial energy will be the rotational energy of the ruler after impact and the final energy will be the GPE at the ruler-clay system’s maximum height:

Conclusion:

Overall, this lab was a success. We had a ridiculously small percent error of .06%. However, there are always random and systematic errors that occur in our labs. Some of the errors in the lab include the resistance from outside forces such as the friction at the pivot and air drag. Also when marking the maximum height of the ruler-clay system on LoggerPro we don’t get the true maximum height since our video only will give us the frame before and the frame after max height. Treating the clay as a point mass also skewed our data since it was really more of a spherical blob. One interesting thing to point out is that, theoretically, the experimental calculation should have had a smaller height due to the resistance of outside forces decreasing its overall energy however that was not the case.

Partners: Chong Li, Aiqi You

Theory/Introduction:

In this lab we are applying a known torque to an object that can rotate and are measuring the object’s angular acceleration. This is done with a Pasco rotational sensor like the one shown below:

The Pasco rotational sensor helps provide a frictionless rotational environment using air pressure. It is the same concept as the air track equipment we’ve used in previous labs.

We will do this lab with several configurations of disks.

By obtaining the angular velocity vs. time graph of a disk we can find it’s angular acceleration by taking the slope of the graph. We can see it’s angular acceleration as it turns clockwise and as it turns counter clockwise.

Going into this lab we are assuming that there is no frictional torque in the system, even though there is some from the inertia/friction from the pulley and friction from the disks.

Experimental Procedure:

We will be using two types of disks, a steel disk and a aluminum disk.  We got the weight and diameter of each disk and the large and small torque pulleys. We also got the weight of the hanging mass. Since the sensor hooked up to LoggerPro goes by the amount of marks on the disk, and there are 200 marks on the disks we are using, we had to to go into the sensor settings and set the equation to 200 counts per rotation. We also made sure the hose clamp is open on the bottom so that the bottom disk will rotate independently from the top. To obtain the most optimal frictionless environment we could get, we cleaned the disks with alcohol. To test the independent rotation of each disk we turned on the apparatus by flipping the compressed air switch on, held the bottom disk down, spun the top disk, and moved away from the apparatus to see if the bottom disk was influenced by the top disk at all. With the string wrapped around the torque pulley and the hanging mass at it’s highest point we could start the experiment.

	Diameter (mm)	Mass (g)
Top Steel Disk	121.3	1359.9
Bottom Steel Disk	121.3	1345.9
Top Aluminum Disk	121.3	465.3
Smaller Torque Pulley	24.8	10
Larger Torque Pulley	48.8	36.2

Trial 1, 2, and 3: Effects of changing the hanging mass

Trial 1 and 4: Effects of changing the radius at which the hanging mass exerts a torque

Trial 4, 5, and 6: Effects of changing the rotating mass.

We were given this prompt to fill out which includes all the variations of experiments we will be doing:

Ideally the graphs would show one full cycle (a down and up phase):

However, in order to get a trend of how accurate the angular acceleration on graphs are going to be for the future experiments we made a graph for experiment #1 that showed a velocity vs. time graph after three full cycles instead of just one:

Over time the angular acceleration of the up and down phases seem to decrease. This makes sense since there is friction in the system.

After getting the data we went on to do some analysis.

Analysis:

From the data we are able to determine the moment of inertia of each of the disks (or disk combinations).

Using Newton’s 2nd Law we can set up some equations to get the Inertia of the disk:

*assuming counter clockwise is positive and clockwise is negative

Using this formula we’re are able to make a theoretical vs. experimental value table for the experiments:

	Theoretical (kg*m*m)	Experimental (kg*m*m)
Trial 1: Steel Disk	.002501	.002643
Trial 2: Steel Disk (2x h_mass)	.002501	.002667
Trial 3: Steel Disk (3x h_mass)	.002501	.002702
Trial 4: Steel Disk (large pulley)	.002501	.002216
Trial 5: Aluminum Disk (large pulley)	.00085578	.00097
Trial 6: Aluminum +Steel Disk (large pulley)	.00335693	.004816

 

Conclusion:

Overall, this experiment was successful. One thing to notice from experiment #1 graph is that there is a downhill trend in acceleration as the experiment goes on. This means that there is some loss of energy in the system due to some outside forces. The biggest forces affecting the system were friction from the pulley and friction from the disks. Due to this loss of friction it was assumed the experimental values inertia would be greater than that of the theoretical values since the angular acceleration would be lower than it should be.

This lab showed some interesting properties of angular acceleration. One trend from the experimental values from #1 and #3 show that smaller torque pulleys produce a smaller angular acceleration than larger pulleys. Another trend from experiment #1-3 show that a greater hanging mass produces a greater angular acceleration. Another trend from experiments #4-6 show that a greater disk mass causes a decrease in angular acceleration.

One trend with experiment #1-3 shows an increase in experimental inertia with an increase in mass. Experiments #1 and #4 show a decrease in experimental inertia with a larger torque pulley.   Experiments #4-6 show an increase in inertia with an increase in torque.

Name: Aaron Nguyen

Partners: Chong Li; Aiqi Li

 

Theory/Introduction:

The purpose of this lab is to determine  if  a 2-D collision between two balls is elastic. The two things that make a collision elastic is the conservation of both momentum and kinetic energy  so in order to determine elasticity we will have to see if these two variables are conserved before and after the collision. In the experiment for this lab, we will be videotaping the collision between a steel ball and a glass ball from a bird’s eye viewpoint. Using LoggerPro to plot the position of the ball we will be able to get the velocity of each ball. In order to check for conservation we will make two graphs: kinetic energy vs. time and momentum vs. time. If momentum  and kinetic energy is conserved, both graphs should emulate a horizontal line since the total amount momentum/KE will be constant throughout the experiment.

 

Experimental Procedure/Apparatus:

To set up the experiment we were provided a few materials for the lab. We were given one steel ball, one glass ball, leveled glass table, and a selfie stick. In order to achieve a bird’s eye view we hooked up the selfie stick up to a pole stand and adjusted our phone to the proper top view. Before starting the lab we made sure the table was leveled also. The 2-d collision we will be simulating is the collision between a glass ball at rest and a steel ball rolling towards it. In order to make sure we had enough frames to record the position we used the slow-mo setting on our phone(240 fps). In order to get a distance of reference between the collisions we put a ruler in the background of our video. After setting up this lab we pressed record on the phone and rolled the steel ball into the glass ball (An ideal collision should make the glass ball roll of a decent angle from the trajectory of the other ball).

After capturing the collision on video we uploaded it to LoggerPro. Since LoggerPro doesn’t know the real time of the collision we had to edit the movie. Under “options” we go to movie “movie options” the choose to “Override frame rate” to 240 fps. Under “video analysis” we chose to advance the frames by 4 after each plotted point. We also gave the video a reference distance by scaling the length of the ruler to .3048 m.

We then rewound the video to the near beginning, right after the steel ball had left my hand and proceeded to plot the position of the steel ball using the “Add Point” button. We treated the center of the ball as the position.  After plotting the steel balls position we clicked the “set point series” button, then “add point series”. The series   X 2 and Y 2 should show up as selected. Once again we clicked the “add point” button and proceeded to plot the position of the glass ball. Even though it was standing still for a part of the video we still rewound to the same frame where the steel ball had just left my hand.

After plotting both positions the picture should look something like the one below:

Analysis:

 

Now that we have all the data we need we made new calculated columns for both kinetic energy and momentum.

Kinetic energy was made by adding the two individual kinetic energies of the balls together:

Momentum was made by adding the two individual momentum of the balls together:

 

Kinetic Energy vs. time graph:

Momentum vs. time graph:

Since both graphs show a relatively horizontal plots we can say that this 2- d collision is most likely elastic.

Although we verified that the collision was elastic, Professor Wolf also wanted us to plot a center of mass position vs. time graph and center of mass velocity vs. time graph of the system.

In order to get the position of the center of mass we employed the center of mass formula we learned from the videos into our lab:

In order to get the expression for velocity we used our knowledge of calculus, since we know the derivative of position is velocity we used the derivative function in LoggerPro on our x(center mass) to make a new calculated column for x  (center mass) velocity. We did the same for the y-positions.

 

After we had the new calculated columns made, we made the graphs for center of mass position vs. time and center of mass velocity vs. time:

The astonishing discovery that should be taken from these graphs is that when following the objects’ center of mass, the position is moving at a constant rate, or in other words, the velocity is constant, even after collision.

 

 

Conclusion:

Although this lab went fairly well it was not perfect. One of the systematic errors that caused this was the fact that when plotting the position of the balls, it is impossible to be completely accurate due to the level of precision needed to click the center of the ball at each frame. Another systematic errors that occurred in the lab was during the collision of the balls. There is a loss of energy after impact because the glass ball would slide before/while rolling. This results in a loss of energy due to kinetic friction, not to mention the loss of energy from other external forces such as air resistance. Another systematic error that came from this lab was the fact that there is some distortion in camera lenses. Since camera lenses capture light from a single point, light comes at the lens at different angles resulting in things farther away from the center of the video to seem to move slower than they actually are.

One thing to note is that even  though in this lab the collision proved to be relatively elastic it does not mean that other types of collisions between the two balls will be elastic. For example, if both ball were rolling toward each other and collided, even though momentum would conserved there would be a loss of kinetic energy in the system since both ball lost velocity after the collision occurred. What made the collision in this experiment elastic was the fact that one ball was standing still while the other one was rolling towards it.

Name: Aaron Nguyen

Partners: Jason Seika and Antonio Baltazar

 

Introduction/Theory:

The purpose of this lab is to verify that conservation of energy can be applied to the system in the lab.

In this lab we will be dealing with a cart with a magnet on it that is approaching a fixed magnet of the same polarity all taking place on a frictionless, horizontal surface. When the cart is at its closest to the fixed magnet (right before it rebounds back), all the kinetic energy is stored as potential energy in the magnet. After the magnet rebounds back the magnetic potential energy is transformed back into kinetic energy.

We will verify that conservation of energy can be applied by making a single graph showing KE, PE, and total energy of the system as a function of time.

Graphing the kinetic energy vs. time of the system is relatively easy since all we need in the mass and velocity of the cart during the experiment.

The difficulty of this lab is graphing the magnetic PE vs. time graph since we don’t have an equation for magnetic PE. Since this system has a non-constant PE we will have to use calculus to develop an equation for the magnetic PE. We will be using this equation for the non-constant PE where r is the separation distance:

With this equation set up, the new challenge is to find what our force equation, F(r), would be. To find F(r) Professor Wolf gave us the power law equation:

Which when plugged into the equation:

Now that we have a good equation for magnetic PE we have to find what A and B are. If we know the force of the magnet and separation distance we can make a F(r) vs r graph in LoggerPro and make the plot fit the identical LoggerPro equation, . This power fit will give the A and B we need to put in our power law equation.

 

Apparatus/Experimental Procedure:

To simulate a cart on a frictionless surface we used a glider cart on an air track. On the glider was the magnet. At the end of the air track was the other magnet. In order to  get multiple points for the force vs separation graph we used our knowledge of Newtons Laws. We knew that on an angled track when the cart at rest is held up by the magnets’ repulsion, we could make an equation that would let us construct the graph. The overall net force would give us the equation: F=mgsinθ . Different angles would give us different r and F(r), the points we needed to make the graph. To record r we used a caliper and to record the angle we used a protractor. Recording the r at five different angles gave us the following table:

	θ	r	F(r)
Trial #1	2 degrees	.0391 m	.12 N
Trial #2	18 degrees	.0166 m	1.06 N
Trial #3	21 degrees	.0143 m	1.23 N
Trial #4	24 degrees	.0137 m	1.4 N
Trial #5	27 degrees	.0106 m	1.56 N

 

Plugging F(r) and r into the F(r) vs r graph and using our given power law equation gave us the following graph:

After we got our A and B we proceeded to run the main experiment.

Before pushing the cart towards the track magnet we first set-up some things. Since the motion detector would calculate the distance between the motion detector and the cart we had to make a new calculated column for “r” where the motion detector would record the distance between the two magnets. We also set up the calculated columns for KE, magnetic PE, and total energy. Their expressions come from the equations:

After all the calculated columns were set up we did the experiment. We pressed record on LoggerPro and pushed the cart to a speed so that when the magnet repelled the cart, the two magnets didn’t bump into each other.

After we had a graph for the experiment we made the y-axis have three of our calculated columns, KE, MPE, and Total Energy. The x-axis was time.

Analysis and Conclusion:

Our graph makes sense. As kinetic energy increases magnetic potential energy decreases and visa versa. However, there are some trends in the graph that should be addressed. The total energy is fairly horizontal as it should be due to conservation of energy but it seems to have a downward trend. This is most likely due to the systematic error that there is a loss in energy over time from external factors such as air resistance and the friction in the air track. Also an alarming discrepancy is that there is a large spike in total energy during the carts reverse in direction. This could be due to the fact that a small difference in how far “r”  when the cart is at max PE would greatly affect the experiment. Looking back to our equation for MPE, a change in the r value would significantly affect the amount of magnetic PE calculated. A way we could’ve reduced the random error in this lab was by plotting more points for the F(r) vs r graph so we have a more accurate power formula fit. With this lab we were able to help verify that the law of conservation of energy can be applied to magnets.

 

 

 

 

 

 

 

Name: Aaron Nguyen

 

Theory/Introduction:

In this lab we are exploring the law of conservation of energy in a vertically oscillating spring-mass system.

The system will consist of a spring oscillating back and forth with a mass attached to the bottom. In the system to make calculations simpler we assumed that the gravitational PE = 0 at the ground.

We know  from the law of conservation of energy that

We also know that the total energy of the system is the sum of all the energies involved in the system. As the spring oscillates we know that there is three energies from the spring: Kinetic Energy, Gravitational Potential Energy, and its Elastic Potential Energy. However, we also must also account for the two energies from the mass attached to the bottom of the spring: Kinetic Energy and Gravitational Potential Energy. Putting this all into an equation for total energy we can say:

In order to get the Total Energy equation into components we can find, we have to breakdown the GPEs, KEs, and EPE of the equation:

Adding these broken down parts together and rearranging it to fit into the KE, GPE, and EPE for the entire system gets us:

or

 

The components we will need to find are “k”, “x”, “v”, “m_spring”, and “m_mass”.

Apparatus/ Experimental Procedure:

To start we got the mass of the spring, 159.6 g.

This lab has a very simple set up:

We mounted a table clamp with a vertical rod to the table. A horizontal rod was then mounted to the vertical rod. A spring was hooked onto the horizontal pole and hung directly above a motion detector. A 100g mass was attached to the bottom of the spring. The bottom of the mass was the surface area that the motion detector was recording.

To calculate the spring constant k we used the equation:

At a hanging mass of 100 g, the spring stretches .1875 m from its resting point.

At a hanging mass of 300 g, the spring stretched .375 m from its resting point.

The (change in weight of hanging mass)/(change in stretch of spring) gets us a k value of 5.23.

After getting the spring constant we could now begin the oscillation documenting of the lab. We made the hanging mass a total of 250 g. To get a good oscillation we pulled the spring down by 10 cm, let go, then pressed record on LoggerPro.

“v” is already given to us, the variable in LoggerPro “velocity”.

To calculate “x”, or the stretch of the spring, we made a new calculated column in LoggerPro labeled “stretch”. The expression for “Stretch” was made by measuring the distance from the motion detector up to the bottom of the hanging mass at the springs resting position and subtracted that by the variable “position”.

Analysis:

After having all the components we needed to make the GPE, KE, and EPE of the system we made the graphs of each of them vs. time. To do so we had to making calculated columns for each of them:

Then we made KE, GPE, and EPE vs. y and vs. v graphs to check if our data made sense:

The graph for GPE vs. y makes sense since as the spring goes up the GPE should increase due to the height from the ground becoming larger.

The graph for GPE vs. v makes sense since as the spring oscillates the graph would repeat as shown from the traced ellipses.

The graph for KE vs. y makes sense since as the spring goes up the KE would increase, but then decrease after the spring begins to slow down and compress.

The graph for KE vs. v makes sense since the relationship between KE and v is similar to a parabola.

The graph for EPE vs. y makes sense since as the spring goes up the EPE would decrease due to lack of stretch.

The graph for EPE vs. v makes sense since as the spring oscillates the graph would repeat as shown from the traced ellipses.

To observe the Total Energy vs. time graph we had to make a new calculated column called Esum and made Esum equal to the sum of all the energies in the system, “KE+GPE+EPE”. Then we added Esum to the y-axis of the graph.

 

The total energy vs. time graph depicts the total energy as a wave when logically it should be a straight horizontal line. By taking the average from peak to peak of the curve (one full oscillation) we get a total energy of 2.6 J. The total energy vs. position graph depicts a more linear-like curve.

Conclusion:

Our lab was fairly successful in demonstrating the law of conservation of energy, but as seen from the total energy vs. time graph being a curve besides a horizontal line, there were some discrepancies involved in this lab. A systematic error that affected the lab was the sway of the spring as it was oscillating. The sway from left to right affected the data points collected by the motion detector. Another systematic error would be the fact that energy is not really conserved in our system. Since there is some non conservative work done on the system such as air resistance and friction in the coils of the spring the energy would be lost as time passes.

 

 

 

 

Name: Aaron Nguyen

Partners: Daniel and Vanessa

 

Theory/Introduction:

The Work-Energy Theorem states that the work done on an object by a net force equals the change in kinetic energy of the object:

W = KE_f – KE_i

The purpose of this lab is to explore the relationship of the Work-Kinetic Theorem with three individual cart experiments.

Experiment #1: We used a system where a constant force is applied to a cart that is initially at rest. According to the theorem the the work done on the cart by the force should equal the kinetic energy acquired by the cart at any point. To help prove the theorem we calculated the left side and right side of the equation separately from our data collected from the experiment.

We calculate the work done on the cart by making a force vs. position graph and taking its area under the curve (Concept: Work=F*d).

We calculated the change in kinetic energy by recording the initial and final velocity of the cart and plugged it into the formula: mv_f ²  – mv_i ²

Experiment #2: We calculated the work done when a non-constant force is applied to the cart. Similarly to experiment #1, we made a force vs. position graph and took the area under the curve.

Experiment #3: We calculated the work done when the cart undergoes a non constant acceleration from rest. Similarly to experiment #1, we are compared the change in kinetic energy and the work done, but this time at three different intervals.

 

Apparatus/Procedure:

 

Experiment #1: To find the work done by a constant force we will be using a motion sensor, force sensor, cart, track, pulley, LoggerPro, and hanging mass:

To record the constant force acting on the cart we will be attaching a force sensor onto it. To simulate the constant force acting on the cart we used a cart-pulley system where one end of the string is attached to the force sensor while the other is attached to a hanging mass. The constant tension in the string will pull the hanging mass a set distance.

To record the position of the cart we will be using a motion sensor that will be placed at the end of the track.

To collect the data on LoggerPro we set the cart at around 15 cm away from motion sensor, hit collect, then let the tension in the string pull the cart.

Experiment #2: To calculate the work done by  a non-constant force we used a motion sensor, force sensor, cart, track, pole, clamp, spring, and LoggerPro:

To simulate a non constant force we used a spring that was attached to the force sensor on the cart. The other end of the spring was attached to a clamped pole. Since in this experiment the cart was going the opposite way we changed the positive-direction to be towards the sensor instead of the default (away from the sensor). After the system was set up we pressed collect on LoggerPro and slowly pushed the cart from it’s resting position toward the motion sensor.

Experiment #3: We used the same set up as experiment #2, but we changed the motion sensor back to where the positive-direction was away from the motion detector. This time we pulled the cart a set distance, pressed collect, then let go of the cart.

 

Analysis:

Experiment #1:

After recording our data into logger pro we made a force vs. position graph. We also needed to graph the kinetic energy and since LoggerPro doesn’t give is an option to select kinetic energy as a y-axis we had to implement the equation for kinetic energy into LoggerPro which was mv ² . We added kinetic energy into the y-axis of the force vs. position graph. By taking the integral of the curve we are able to get the work done on the cart over a set distance (left-side of the equation). By examining the y value of the kinetic energy curve at the same distance we were able to get the acquired kinetic energy at that point (right-side of the equation). After we compared the percent difference between work done and the change in kinetic energy.

*note: Unfortunately I cannot find the picture that shows the integral of the force curve and the y-value of the kinetic energy curve so we could not compare the values.

Experiment #2:

After recording the data into LoggerPro we made a force vs. time graph:

The work done on the cart was the integral of the curve which was 0.321 J. By taking the slope of the line we are able to get the spring constant of the spring, “3.3”. We know the slope is equal to the spring constant from the following derivation:

Experiment #3: 

After recording the data into LoggerPro we made a force vs. time graph. To explore the reaches of the work-kinetic energy theorem we took the work done along with its change in kinetic energy over three different intervals:

 

	Work (Integral)	Kinetic Energy	Percent Difference
Interval #1	-0.4538 J	0.522 J	14.0%
Interval #2	-0.322 J	0.352 J	8.9%
Interval #3	-0.1677 J	0.199 J	17.1%

 

Experiment #4:

After finishing our experiments we ended up watching a video from Professor Wolf. In the video. the professor uses a machine to pull back on a large rubber band. The force on the rubber band was recorded by an analog force transducer onto a graph. The stretched rubber band is then attached to a cart of known mass. The cart, once released, passes through two photo gates a given distance apart.

From the video we were asked to calculate the work done and the kinetic energy of the cart and compare the results just like how we did in the previous experiments.

By making a careful sketch of the force vs. position graph shown in the video and taking the area underneath it by chopping it up into rectangles and trapezoids, we were able to determine the work done by the machine stretching the rubber band.

Adding up the area of all the rectangles and trapezoids gives us a work of 22 J.

To calculate the kinetic energy we need the velocity  and mass of the cart to plug into the formula: mv_f ²

We were given the mass of the cart: 4.3 kg

We were not given the velocity of the cart, however, we were given the time interval of the cart passing from one photo gate to the other (.0455 sec) and the distance between each photo gate (.15 m). With these two values we are able to calculate the velocity since: 

This gives us a kinetic energy of 23.84 J.

The percent difference between these two values is 8%

Conclusion:

Overall our results from our experiments were fairly accurate, but not ideal. Usually for our experiments a percent difference of 5% or less would indicate a well done experiment however ours was unfortunately not in that range. A trend that seemed to occur in the data from experiment #3 was that the calculate kinetic energy was greater than the work done for each experiment. Since only three intervals were taken it could quite easily be a coincidence. Some systematic errors that could have increased the percent difference was the friction between the wheels of the cart and the track. This would decrease the value of kinetic energy.

 

 

Name: Aaron Nguyen

Partner: Vanessa Gonzalez and Daniel Agee

 

Apparatus:

The apparatus used for this lab was set up before class:

It is an electric motor mounted on a surveying tripod. Connected to the motor is a long vertical shaft that is connected to a ruler. The ruler is attached to a string with a mass at the end of it. During the experiment the motor spin with a constant angular velocity, ω. There will also be an angle between where it was at rest (vertical line),  and the line it makes when it is at a constant angular velocity labeled as, θ. The height of the stopper when it is at a constant speed will be recorded with the help of a ring stand with a horizontal piece of paper sticking out of it.

 

Introduction/Theory:

The purpose of this lab is to find a theoretical model for the relationship between the angle of the string, θ, and the angular velocity, ω, and compare this model with the actual angular velocity.

The illustration of the apparatus below will be used to explain how to find the angle and angular velocity:

We can find a model for ω by taking a free body diagram of the stopper during motion and manipulating its x and y axis equations:

We can find the angle, θ, by using trigonometry. if we know the height of the apparatus,”H”, and height of the stopper, “h”, and the length of the string,”L”, we can set up the equation:

 

 

Experimental Procedure:

We ran a total of 7 experiments in this lab. Professor Wolf changed the voltage of the electric motor for each experiment so that we would have several angular velocities and angles.

The height of the apparatus and the length of the string were measured with two meter stick since they were both too long to be measured with only one.

The height of the stopper during motion was a bit trickier to get. Since it’s hard to get the height of the stopper during rotation we used the ring stand mentioned earlier. By slowly inching the paper higher and higher on the ring stand, it eventually gets hit by the stopper. The point of impact is essentially the height of the rubber stopper. A meter stick was used to record the height.

The actual angular velocity was obtained by recording the amount of time 10 full rotation would take.  Knowing the time would let us set up the formula (2π)(10 rotations)/ (time) to give us the actual angular momentum.

This stopper height and time for 10 rotations were recorded for all seven experiments.

Data/Calculations: The data and calculations for the theoretical ω, actual ω, and θ:

Analysis:

To compare our actual angular velocity to our theoretical velocity we made an actual vs theoretical velocity graph:

By using a linear fit line we see that the slope is 0.879.  Ideally the slope should be 1.0 since actual velocity should equal theoretical velocity. However, since the experiment is not meant to show complete accuracy, we know it wouldn’t be exactly a 1:1 ratio.

Conclusion:

Although our theoretical and actual velocities were not quite equal to each other, they were close enough to say our angular velocity/angle model is likely accurate. The slope of 0.879 could have been due to a few systematic errors. One example being the air resistance the stopper endures during it’s rotation. The air resistance causes the radius to decrease since the string is being dragged behind. By ignoring the decreased radius in our calculations, the value of the theoretical angular velocity would be higher than what it should have been. Not accounting for this error would effectively make our slope value lower.  Another systematic error that could have tampered with our results was our method to obtain the height of the stopper. We weren’t quite sure where the exact point of impact was in the paper so we had to guess. To reduce this error we could have raised the paper even slower up the ring stand until it brazed the top of the paper, but for the sake of time we didn’t go that slow. Instead of the point of impact being at the top of the paper, the point of impact was somewhere in the middle of the paper.

 

Name: Aaron Nguyen

Partners: Daniel and Vanessa

 

Theory/Introduction: The purpose of this lab is to verify the equation:

To verify this equation we will be calculating both sides of the equation.

We will be using this apparatus to calculate F(centripetal) and (mv^2)/r :

The apparatus will mimic the circular rotation of the object connected to the spring. The object will be treated as a point mass and the horizontal distance it is away from the pivot will be treated as the radius of rotation.

In order to utilize this apparatus we will be integrating concepts of centripetal force and Newton’s laws. When we spin the object around the pivot until it becomes vertical with the table we are able to say F(centripetal)=F(spring).

To get F(centripetal), which turns out to be F(spring), we can attach a string to the other side of the object and attach the other end of the string to a pulley-hanging mass system. With the right amount of hanging mass the object will be perpendicular to the floor. The weight of the hanging mass when the object is perpendicular will be equal to the F(spring) which is equal to F(centripetal), or as written in an equation:

F(centripetal) = F(spring) = Tension = Weight of Hanging Mass

 

To get (mv^2)/r we need to calculate the constant tangential velocity of the object during its rotation, the radius of the rotation, and the mass of the object. The mass and radius can be measured but the velocity is a bit tricky to get:

According the the equation, in order to get the velocity, we will need to get the time it takes for the object to complete a full rotation.

In order to verify the equation

We will run three experiments. The first experiment will just the mass at a set radius. The second experiment will be a greater mass at the original radius.  The third experiment will be the original mass at a greater radius.

Experiment/Apparatus:

Experiment #1:

F(centripetal) : Since we know “F(centripetal) = weight of the hanging mass” when the object is at vertical, we set up the pulley-hanging mass system and kept adding mass to the hanging mass until the object was at vertical.  The total mass of the hanging mass was multiplied by gravity to get F(centripetal).

(mv^2)/r : To get “(mv^2)/r” we had to get radius, mass, and the time for one full rotation when the object is at vertical. To get the radius we measured from the center of the pivot to the string that is holding up the object. To get the mass of the object we just read the description that was engraved on its surface. To get the time it takes for one rotation we actually recorded the amount of time it takes for the object to complete twenty rotations and divided that time by 20 in order to get a more accurate time interval.

Experiment #2:

The same process from experiment #1 was done but with a greater mass this time. To simulate a greater mass we were able to unscrew the top of the object, slide a 150 gram mass between the object and the top, then screw the top back in so that the added mass was wedged between the two surfaces.

Experiment #3:

The same process from experiment #1 was done but with a greater radius this time. To obtain a greater radius we unscrewed the top part of the pivot which allowed the part holding the radius to extend past its current state.

 

Data:

	Experiment #1	Experiment #2	Experiment #3
Mass of Object	0.447 kg	0.597 kg	0.447 kg
Mass of Hanging Mass	0.270 kg	0.270 kg	0.420 kg
Time of One Rotation	1.06 s	1.08 s	1.32 s
Radius	0.219 m	0.219 m	0.256 m

Analysis:

After getting all our data for each experiment we could plug it all in with the equations we had derived from earlier.

Calculations for the left side of the equation above:

Calculations for the right side of the equation above:

When comparing the left to the right side we can see there is a bit of a difference between the left and right side of the equation. Experiment #1 had a percent difference of 26.2%. Experiment #2 had a percent difference of 31.2%, and experiment #3 had a percent difference of 36.7%.

Conclusion: Given the percent difference of our values for each experiment we were not able to help verify that

but since our values landed around the same area we could say they at least pointed toward the equation being true. The large percent difference in each experiment was expected due to the precision on some parts of the experiment. I believe one of the biggest sources for this inaccuracy was due to the random error produced when we rotated the pivot until the object became vertical. The object was spinning so fast that it was hard to tell whether the object was vertical or not which would affect the time of one rotation. We tried to reduce this error by taking the time of 20 rotations and doing three experiments, but getting the object to stay consistently vertical is quite difficult. A systematic error that could have affected the end results is the fact that the object is not a point mass. We treated the center of mass as the point mass, but not accounting for the mass being spread out could have affected the experiment greatly.